11. Taylor Series
Exercises
-
\(\begin{aligned} f(x)=\dfrac{1}{x} \end{aligned}\)
\(\displaystyle T_4\left(\dfrac{1}{x}\right)\approx\dfrac{1}{2}-\dfrac{1}{4}(x-2) +\dfrac{1}{8}(x-2)^2-\dfrac{1}{16}(x-2)^3+\dfrac{1}{32}(x-2)^4\)
The function, its derivatives and their values at \(x=2\) are: \[\begin{aligned} f(x)&=\dfrac{1}{x} &f(2)&=\dfrac{1}{2} \\ f'(x)&=-x^{-2} &f'(2)&=-\dfrac{1}{4} \\ f''(x)&=2x^{-3} &f''(2)&=\dfrac{1}{4} \\ f'''(x)&=-6x^{-4} &f'''(2)&=-\dfrac{3}{8} \\ f^{(4)}(x)&=24x^{-5} \qquad &f^{(4)}(2)&=\dfrac{3}{4} \end{aligned}\] We plug these into the Taylor polynomial centered at \(x=2\): (Don't forget the factorials.) \[\begin{aligned} f(x)&\approx f(2)+f'(2)(x-2)+\dfrac{f''(2)}{2}(x-2)^2 \\ &\quad+\dfrac{f'''(2)}{3!}(x-2)^3+\dfrac{f^{(4)}(2)}{4!}(x-2)^4 \\ \dfrac{1}{x}&\approx\dfrac{1}{2}-\dfrac{1}{4}(x-2)+\dfrac{1}{8}(x-2)^2 \\ &\quad-\dfrac{1}{16}(x-2)^3+\dfrac{1}{32}(x-2)^4 \end{aligned}\]
dd
-
\(f(x)=\ln(x)\)
\(\displaystyle T_4\approx\ln(2)+\dfrac{1}{2}(x-2)-\dfrac{1}{8}(x-2)^2 +\dfrac{1}{24}(x-2)^3-\dfrac{1}{64}(x-2)^4\)
The function, its derivatives and their values at \(x=2\) are: \[\begin{aligned} f(x)&=\ln(x) &f(2)&=\ln(2) \\ f'(x)&=(x)^{-1} &f'(2)&=\dfrac{1}{2} \\ f''(x)&=-(x)^{-2} &f''(2)&=-\dfrac{1}{4} \\ f'''(x)&=2(x)^{-3} &f'''(2)&=\dfrac{1}{4} \\ f^{(4)}(x)&=-6(x)^{-4} \qquad &f^{(4)}(2)&=-\dfrac{3}{8} \end{aligned}\] We plug these into the Taylor polynomial centered at \(x=2\): (Don't forget the factorials.) \[\begin{aligned} f(x)&\approx f(2)+f'(2)(x-2)+\dfrac{f''(2)}{2}(x-2)^2 \\ &\quad+\dfrac{f'''(2)}{3!}(x-2)^3+\dfrac{f^{(4)}(2)}{4!}(x-2)^4+\cdots\\ T_4f&\approx\ln(2)+\dfrac{1}{2}(x-2)-\dfrac{1}{8}(x-2)^2 \\ &\quad+\dfrac{1}{24}(x-2)^3-\dfrac{1}{64}(x-2)^4 \end{aligned}\]
dd
-
\(f(x)=xe^x\)
\(\displaystyle T_4(xe^x) \approx2e^2+3e^2(x-2)+2e^2(x-2)^2+\dfrac{5}{6}e^2(x-2)^3+\dfrac{1}{4}e^2(x-2)^4\)
The function, its derivatives and their values at \(x=2\) are: \[\begin{aligned} f(x)&=xe^x &f(2)&=2e^2 \\ f'(x)&=xe^x+e^x &f'(2)&=3e^2 \\ f''(x)&=xe^x+2e^x &f''(2)&=4e^2 \\ f'''(x)&=xe^x+3e^x &f'''(2)&=5e^2 \\ f^{(4)}(x)&=xe^x+4e^x \qquad &f^{(4)}(2)&=6e^2 \end{aligned}\] We plug these into the Taylor polynomial centered at \(x=2\): (Don't forget the factorials.) \[\begin{aligned} f(x)&\approx f(2)+f'(2)(x-2)+\dfrac{f''(2)}{2}(x-2)^2 \\ &\quad+\dfrac{f'''(2)}{3!}(x-2)^3+\dfrac{f^{(4)}(2)}{4!}(x-2)^4 \\ xe^x&\approx 2e^2+3e^2(x-2)+2e^2(x-2)^2 \\ &\quad+\dfrac{5}{6}e^2(x-2)^3+\dfrac{1}{4}e^2(x-2)^4 \end{aligned}\]
dd
-
\(f(x)=e^{2x}\), centered at \(x=1\)
\(\displaystyle e^{2x}=\sum_{n=0}^\infty \dfrac{2^ne^2}{n!}(x-1)^n\)
\(R=\infty\)The function, its derivatives and their values at \(x=1\) are: \[\begin{aligned} f(x)&=e^{2x} &f(1)&=e^2 \\ f'(x)&=2e^{2x} &f'(1)&=2e^2 \\ f''(x)&=4e^{2x} &f''(1)&=4e^2 \\ f'''(x)&=8e^{2x} &f'''(1)&=8e^2 \\ f^{(4)}(x)&=16e^{2x} \qquad &f^{(4)}(1)&=16e^2\\ \end{aligned}\] We plug these into the Taylor polynomial centered at \(x=1\): (Don't forget the factorials.) \[\begin{aligned} f(x)&=f(1)+f'(1)(x-1)+\dfrac{f''(1)}{2}(x-1)^2 \\ &\quad+\dfrac{f'''(1)}{3!}(x-1)^3+\dfrac{f^{(4)}(1)}{4!}(x-1)^4+\cdots \\ e^{2x}&=e^2+2e^2(x-1)+2e^2(x-1)^2 \\ &\quad+\dfrac{4}{3}e^2(x-1)^3+\dfrac{2}{3}e^2(x-1)^4 \end{aligned}\] To express the series in summation form with the general term, we need to go back and generalize the derivatives to the \(n^\text{th}\) derivative. \[ f^{(n)}(x)=2^ne^{2x} \qquad f^{(n)}(1)=2^ne^2 \] Thus, the Taylor Series is \[\begin{aligned} f(x) &=\sum_{n=0}^\infty \dfrac{f^{(n)}(1)}{n!}(x-1)^n \\ e^{2x} &=\sum_{n=0}^\infty \dfrac{2^ne^2}{n!}(x-1)^n \end{aligned}\] To find the radius of convergence, we use the ratio test: \[\begin{aligned} \rho&=\lim_{n\to\infty}\dfrac{|a_{n+1}|}{|a_n|} =\lim_{n\to\infty}\dfrac{2^{n+1}e^2|x-1|^{n+1}}{(n+1)!} \dfrac{n!}{2^ne^2|x-1|^n} \\ &=\lim_{n\to\infty}\dfrac{2|x-1|}{n+1}=0 \end{aligned}\] Since \(\rho=0 \lt 1\), the series convergence for all \(x\) and the radius of convergence is \(R=\infty\).
dd
-
\(f(x)=x\cos(x)\), centered at \(x=0\)
\(\displaystyle x\cos(x)=\sum_{k=0}^\infty \dfrac{(-1)^k}{(2k)!}x^{2k+1}\)
\(R=\infty\)The function, its derivatives and their values at \(x=0\) are: \[\begin{aligned} f(x)&=x\cos(x) &f(0)&=0 \\ f'(x)&=-x\sin(x)+\cos(x) &f'(0)&=1 \\ f''(x)&=-x\cos(x)-2\sin(x) &f''(0)&=0 \\ f'''(x)&=x\sin(x)-3\cos(x) &f'''(0)&=-3 \\ f^{(4)}(x)&=x\cos(x)+4\sin(x) &f^{(4)}(0)&=0\\ f^{(5)}(x)&=-x\sin(x)+5\cos(x) \qquad &f^{(5)}(0)&=5 \end{aligned}\] We plug these into the Taylor polynomial centered at \(x=0\): (Don't forget the factorials.) \[\begin{aligned} f(x)&=f(0)+f'(0)(x)+\dfrac{f''(0)}{2}(x)^2+\dfrac{f'''(0)}{3!}(x)^3 \\ &\quad+\dfrac{f^{(4)}(0)}{4!}(x)^4+\dfrac{f^{(5)}(0)}{5!}(x)^5+\cdots \\ x\cos(x)&=x-\dfrac{1}{2}x^3+\dfrac{1}{24}x^5 \end{aligned}\] To find the general term, we generalize the derivatives: \[\begin{aligned} f^{(2k)}(x)&=(-1)^k[x\cos(x)+(2k)\sin(x)] \\ f^{(2k)}(0)&=0 \\ f^{(2k+1)}(x)&=(-1)^k[-x\sin(x)+(2k+1)\cos(x)] \\ f^{(2k+1)}(0)&=(-1)^k(2k+1) \end{aligned}\] Thus, the Maclaurin Series is \[\begin{aligned} f(x) &=\sum_{n=0}^\infty \dfrac{f^{(n)}(0)}{n!}(x)^n \\ x\cos(x) &=\sum_{k=0}^\infty (-1)^k\dfrac{(2k+1)}{(2k+1)!}x^{2k+1} \\ &=\sum_{k=0}^\infty \dfrac{(-1)^k}{(2k)!}x^{2k+1} \end{aligned}\] To find the radius of convergence, we use the ratio test: \[\begin{aligned} \rho&=\lim_{k\to\infty}\dfrac{|a_{k+1}|}{|a_k|} =\lim_{k\to\infty}\dfrac{|x|^{2k+3}}{(2k+2)!} \dfrac{(2k)!}{|x|^{2k+1}} \\ &=\lim_{k\to\infty}\dfrac{|x|^2}{(2k+2)(2k+1)}=0 \end{aligned}\] Since \(\rho=0 \lt 1\), the series convergence for all \(x\) and the radius of convergence is \(R=\infty\).
dd
-
\(\begin{aligned} f(x)=\dfrac{1}{x+1} \end{aligned}\), centered at \(x=-2\)
\(\displaystyle \dfrac{1}{1+x}=\sum_{n=0}^\infty-(x+2)^n\)
\(R=1\)The function, its derivatives and their values at \(x=-2\) are: \[\begin{aligned} f(x)&=(x+1)^{-1} &f(-2)&=-1 \\ f'(x)&=-(x+1)^{-2} &f'(-2)&=-1 \\ f''(x)&=2(x+1)^{-3} &f''(-2)&=-2 \\ f'''(x)&=-3!(x+1)^{-4} \qquad &f'''(-2)&=-3! \\ f^{(4)}(x)&=4!(x+1)^{-5} &f^{(4)}(-2)&=-4! \end{aligned}\] We plug these into the Taylor polynomial centered at \(x=-2\): (Don't forget the factorials.) \[\begin{aligned} f(x)&=f(-2)+f'(-2)(x+2)+\dfrac{f''(1)}{-2}(x+2)^2 \\ &\quad+\dfrac{f'''(-2)}{3!}(x+2)^3+\dfrac{f^{(4)}(-2)}{4!}(x+2)^4+\cdots \\ \dfrac{1}{1+x}&=-1-(x+2)-(x+2)^2-(x+2)^3-(x+2)^4 \end{aligned}\] The \(n^\text{th}\) derivative is \(f^{(n)}(-2)=-n!\). So the Taylor Series is \[\begin{aligned} f(x) &=\sum_{n=0}^\infty \dfrac{f^n(-2)}{n!}(x+2)^n \\ \dfrac{1}{1+x} &=\sum_{n=0}^\infty-(x+2)^n \end{aligned}\] To find the radius of convergence, we use the ratio test: \[ \rho=\lim_{n\to\infty}\dfrac{|a_{n+1}|}{|a_n|} =\lim_{n\to\infty}\dfrac{|x+2|^{n+1}}{|x+2|^n}=|x+2| \] So the series is convergent if \(\rho=|x+2| \lt 1\). Thus the radius of convergence is \(R=1\).
dd
-
\(f(x)=\cos(x)\), centered at \(x=\dfrac{\pi}{2}\)
\(\displaystyle \cos(x)=\sum_{n=0}^\infty \dfrac{(-1)^{n+1}}{(2n+1)!} \left(x-\dfrac{\pi}{2}\right)^{2n+1}\)
\(R=\infty\)The function, its derivatives and their values at \(x=\dfrac{\pi}{2}\) are: \[\begin{aligned} f(x)&=\cos(x) &f\left(\dfrac{\pi}{2}\right)&=0 \\ f'(x)&=-\sin(x) &f'\left(\dfrac{\pi}{2}\right)&=-1 \\ f''(x)&=-\cos(x) \quad &f''\left(\dfrac{\pi}{2}\right)&=0 \\ f'''(x)&=\sin(x) &f'''\left(\dfrac{\pi}{2}\right)&=1 \\ f^{(4)}(x)&=\cos(x) &f^{(4)}\left(\dfrac{\pi}{2}\right)&=0 \end{aligned}\] Thereafter, these cycle every \(4\) derivatives. We plug them into the Taylor polynomial centered at \(x=\dfrac{\pi}{2}\): (Don't forget the factorials.) Notice that the even terms are multiplied by \(0\). \[\begin{aligned} f(x)&=f\left(\dfrac{\pi}{2}\right)+f'\left(\dfrac{\pi}{2}\right)\left(x-\dfrac{\pi}{2}\right) +\dfrac{f''\left(\dfrac{\pi}{2}\right)}{2}\left(x-\dfrac{\pi}{2}\right)^2 \\ &\quad +\dfrac{f'''\left(\dfrac{\pi}{2}\right)}{3!}\left(x-\dfrac{\pi}{2}\right)^3 +\dfrac{f^{(4)}\left(\dfrac{\pi}{2}\right)}{4!} \left(x-\dfrac{\pi}{2}\right)^4+\cdots \\ \cos(x)&=-\left(x-\dfrac{\pi}{2}\right)+\dfrac{1}{6}\left(x-\dfrac{\pi}{2}\right)^3 -\dfrac{1}{120}\left(x-\dfrac{\pi}{2}\right)^5+\cdots \end{aligned}\] To generalize the series, note that only odd powered terms are present and that every other term is negative. Therefore, we can generalize the series as \[ \cos(x) =\sum_{n=0}^\infty \dfrac{(-1)^{n+1}}{(2n+1)!}\left(x-\dfrac{\pi}{2}\right)^{2n+1} \] To find the radius of convergence, use the ratio test: \[\begin{aligned} \rho&=\lim_{n\to\infty}\dfrac{|a_{n+1}|}{|a_n|} =\lim_{n\to\infty}\dfrac{\left|x-\dfrac{\pi}{2}\right|^{2n+3}}{(2n+3)!} \dfrac{(2n+1)!}{\left|x-\dfrac{\pi}{2}\right|^{2n+1}} \\ &=\lim_{n\to\infty}\dfrac{\left|x-\dfrac{\pi}{2}\right|^2}{(2n+3)(2n+2)}=0 \end{aligned}\] Since \(\rho=0 \lt 1\) for all \(x\), the series converges for all \(x\) and the radius of convergence is \(R=\infty\).
dd
-
\(\begin{aligned} \dfrac{1}{1-x} \end{aligned}\)
\(\displaystyle \dfrac{1}{1-x}=\sum_{n=0}^\infty x^n\)
\(R=1\)The function, its derivatives and their values at \(x=0\) are: \[\begin{aligned} f(x)&=\dfrac{1}{1-x} &f(0)&=1 \\ f'(x)&=(1-x)^{-2} &f'(0)&=1 \\ f''(x)&=2(1-x)^{-3} &f''(0)&=2 \\ f'''(x)&=6(1-x)^{-4} &f'''(0)&=6\\ f^{(4)}(x)&=24(1-x)^{-5} \quad &f^{(4)}(0)&=24 \end{aligned}\] We plug these into the Taylor polynomial centered at \(x=0\): (Don't forget the factorials.) \[\begin{aligned} f(x)&=f(0)+f'(0)x+\dfrac{f''(0)}{2}(x)^2 \\ &\quad+\dfrac{f'''(0)}{3!}(x)^3+\dfrac{f^{(4)}(0)}{4!}(x)^4+\cdots \\ \dfrac{1}{1-x}&=1+x+x^2+x^3+x^4+\cdots \end{aligned}\] We can generalize the series as \[ \dfrac{1}{1-x}=\sum_{n=0}^\infty x^n \] To find the radius of convergence, use the ratio test: \[ \rho=\lim_{n\to\infty}\dfrac{|a_{n+1}|}{|a_n|} =\lim_{n\to\infty}\dfrac{|x|^{n+1}}{|x|^n}=|x| \lt 1 \] Therefore, the series is convergent if \(|x| \lt 1\) so \(R=1\).
dd
-
\(f(x)=\ln(1+x)\)
\(\displaystyle \ln(1+x) =\sum_{n=1}^\infty \dfrac{(-1)^{n+1}}{n}x^n\)
\(R=1\)The function, its derivatives and their values at \(x=0\) are: \[\begin{aligned} f(x)&=\ln(1+x) &f(0)&=0 \\ f'(x)&=\dfrac{1}{1+x} &f'(0)&=1 \\ f''(x)&=-(1+x)^{-2} &f''(0)&=-1 \\ f'''(x)&=2(1+x)^{-3} &f'''(0)&=2 \\ f^{(4)}(x)&=-6(1+x)^{-4} \quad &f^{(4)}(0)&=-6 \end{aligned}\] We plug these into the Taylor polynomial centered at \(x=0\): (Don't forget the factorials.) \[\begin{aligned} f(x)&=f(0)+f'(0)x+\dfrac{f''(0)}{2}x^2 \\ &\quad+\dfrac{f'''(0)}{3!}x^3+\dfrac{f^{(4)}(0)}{4!}x^4+\cdots \\ \ln(1+x)&=x-\dfrac{1}{2}x^2+\dfrac{1}{3}x^3-\dfrac{1}{4}x^4+\cdots \end{aligned}\] We can generalize the series as (Notice the \(n=0\) term is omitted because it is \(0\).) \[ \ln(1+x)=\sum_{n=1}^\infty \dfrac{(-1)^{n+1}}{n}x^n \] To find the radius of convergence, use the ratio test: \[ \rho=\lim_{n\to\infty}\dfrac{|a_{n+1}|}{|a_n|} =\lim_{n\to\infty}\dfrac{|x|^{n+1}}{n+1} \dfrac{n}{|x|^n} =|x|\lim_{n\to\infty}\dfrac{n}{n+1}=|x| \lt 1 \] Therefore, the series is convergent if \(|x| \lt 1\) so \(R=1\).
dd,jp
-
\(f(x)=\arctan(x)\)
\(\displaystyle \arctan(x)=\sum_{n=0}^\infty \dfrac{(-1)^n}{2n+1}x^{2n+1}\)
\(R=\infty\)The function, its derivatives and their values at \(x=0\) are: \[\begin{aligned} f(x)&=\arctan(x) &f(0)&=0 \\[8pt] f'(x)&=\dfrac{1}{1+x^2} &f'(0)&=1 \\[8pt] f''(x)&=\dfrac{-2x}{(1+x^2)^2} &f''(0)&=0 \\[8pt] f'''(x)&=\dfrac{6x^2-2}{(1+x^2)^3} &f'''(0)&=-2\\[8pt] f^{(4)}(x)&=\dfrac{24x(-x^2+1)}{(1+x^2)^4} &f^{(4)}(0)&=0 \\[8pt] f^{(5)}(x)&=\dfrac{24(5x^4-10x^2+1)}{(1+x^2)^5} \quad &f^{(5)}(0)&=24 \\[8pt] \end{aligned}\] We plug these into the Taylor polynomial centered at \(x=0\): (Don't forget the factorials.)
Notice that the even degree terms are all \(0\). \[\begin{aligned} f(x)&=f(0)+f'(0)x+\dfrac{f''(0)}{2}(x)^2+\dfrac{f'''(0)}{3!}(x)^3 \\ &\quad+\dfrac{f^{(4)}(0)}{4!}(x)^4+\dfrac{f^{(5)}(0)}{5!}(x)^4+\cdots \\ \arctan(x)&=x-\dfrac{1}{3}x^3+\dfrac{1}{5}x^5+\cdots \end{aligned}\] We can write this series in summation notation as \[ \arctan(x)=\sum_{n=0}^\infty \dfrac{(-1)^n}{2n+1}x^{2n+1} \] To find the radius of convergence, use the ratio test: \[\begin{aligned} \rho&=\lim_{n\to\infty}\dfrac{|a_{n+1}|}{|a_n|} =\lim_{n\to \infty }\dfrac{|x|^{2n+2}}{(2n+2)}\dfrac{(2n+1)}{|x|^{2n+1}} \\ &=|x|\lim_{n\to\infty}\dfrac{2n+1}{2n+2}=|x| \lt 1 \end{aligned}\] Therefore, the series is convergent if \(|x| \lt 1\). So the radius of convergence is \(R=1\)dd,jp
-
In the text, we found the standard Maclaurin series for \(\sin(x)\) and \(\cos(x)\). Here find the Maclaurin series for \(\sinh(x)\) and \(\cosh(x)\) using only the \(4\) facts that \[\begin{aligned} \sinh(0)&=0 \qquad &\dfrac{d}{dx}\sinh(x)=\cosh(x) \\ \cosh(0)&=1 \qquad &\dfrac{d}{dx}\cosh(x)=\sinh(x) \end{aligned}\] (Find the first \(3\) derivatives and the \(n^\text{th}\) derivative, from which you can write out the Maclaurin series.)
-
Find the Maclaurin series for \(\sinh(x)\). Then find its radius of convergence.
By definition, \[ \sinh(x)=\dfrac{e^x-e^{-x}}{2} \qquad \text{and} \qquad \cosh(x)=\dfrac{e^x+e^{-x}}{2} \] but you should not need these to find the Maclaurin series.
\(\begin{aligned} \sinh(x)&=x+\dfrac{x^3}{6}+\cdots \\ &=\sum_{n=0}^\infty \dfrac{1}{(2n+1)!}x^{2n+1} \end{aligned}\)
\(R=\infty\)The function, its derivatives and their values at \(x=0\) are: \[\begin{aligned} f(x)&=\sinh(x) &f(0)&=0 \\ f'(x)&=\cosh(x) &f'(0)&=1 \\ f''(x)&=\sinh(x) \quad &f''(0)&=0 \\ f'''(x)&=\cosh(x) &f'''(0)&=1 \\ f^{(4)}(x)&=\sinh(x) &f^{(4)}(0)&=0 \end{aligned}\] This alternates every other derivative. So we plug them into the Maclaurin series: (Don't forget the factorials.) \[\begin{aligned} f(x)&=f(0)+f'(0)x +\dfrac{f''(0)}{2}x^2 \\ &\quad +\dfrac{f'''(0)}{3!}x^3 +\dfrac{f^{(4)}(0)}{4!}x^4+\cdots \\ \sinh(x)&=x+\dfrac{x^3}{6}+\cdots \end{aligned}\] To generalize the series, notice that all the even derivatives are zero and so only odd powered terms are present. Therefore, we can generalize the series as \[ \sinh(x) =\sum_{n=0}^\infty \dfrac{1}{(2n+1)!}x^{2n+1} \] To find the radius of convergence, we use the ratio test: \[\begin{aligned} \rho&=\lim_{n\to\infty}\dfrac{|a_{n+1}|}{|a_n|} =\lim_{n\to\infty}\dfrac{\left|x\right|^{2n+3}}{(2n+3)!} \dfrac{(2n+1)!}{\left|x\right|^{2n+1}} \\ &=\lim_{n\to\infty}\dfrac{\left|x\right|^2}{(2n+3)(2n+2)}=0 \quad \text{for all} \,x \end{aligned}\] Since \(\rho=0 \lt 1\) for all \(x\), the series converges for all \(x\) and the radius of convergence is \(R=\infty\).
jp
Notice that the series for \(\sinh\): \[ \sinh(x)=\sum_{n=0}^\infty \dfrac{1}{(2n+1)!}x^{2n+1} \] is identical to that for \(\sin\): \[ \sin(x)=\sum_{n=0}^\infty \dfrac{(-1)^{n}}{(2n+1)!}x^{2n+1} \] except that there are no minuses. This is one of the reasons the name hyperbolic sine includes the word sine.
-
Find the Maclaurin series for \(\cosh(x)\). Then find its radius of convergence.
By definition, \[ \sinh(x)=\dfrac{e^x-e^{-x}}{2} \qquad \text{and} \qquad \cosh(x)=\dfrac{e^x+e^{-x}}{2} \] but you should not need these to find the Maclaurin series.
\(\begin{aligned} \cosh(x)&=x+\dfrac{x^2}{2}+\dfrac{x^4}{4!}+\cdots \\ &=\sum_{n=0}^\infty \dfrac{1}{(2n)!}x^{2n} \end{aligned}\)
\(R=\infty\)The function, its derivatives and their values at \(x=0\) are: \[\begin{aligned} f(x)&=\cosh(x) &f(0)&=1 \\ f'(x)&=\sinh(x) &f'(0)&=0 \\ f''(x)&=\cosh(x) \quad &f''(0)&=1 \\ f'''(x)&=\sinh(x) &f'''(0)&=0 \\ f^{(4)}(x)&=\cosh(x) &f^{(4)}(0)&=1 \end{aligned}\] This alternates every other derivative. So we plug them into the Maclaurin series: (Don't forget the factorials.) \[\begin{aligned} f(x)&=f(0)+f'(0)x +\dfrac{f''(0)}{2}x^2 \\ &\quad +\dfrac{f'''(0)}{3!}x^3 +\dfrac{f^{(4)}(0)}{4!}x^4+\cdots \\ \cosh(x)&=x+\dfrac{x^2}{2}+\dfrac{x^4}{4!}+\cdots \end{aligned}\] To generalize the series, notice that all the odd derivatives are zero and so only even powered terms are present. Therefore, we can generalize the series as \[ \cosh(x) =\sum_{n=0}^\infty \dfrac{1}{(2n)!}x^{2n} \] To find the radius of convergence, we use the ratio test: \[\begin{aligned} \rho&=\lim_{n\to\infty}\dfrac{|a_{n+1}|}{|a_n|} =\lim_{n\to\infty}\dfrac{\left|x\right|^{2n+2}}{(2n+2)!} \dfrac{(2n)!}{\left|x\right|^{2n}} \\ &=\lim_{n\to\infty}\dfrac{\left|x\right|^2}{(2n+2)(2n+1)}=0 \quad \text{for all} \,x \end{aligned}\] Since \(\rho=0 \lt 1\) for all \(x\), the series converges for all \(x\) and the radius of convergence is \(R=\infty\).
jp
Notice that the series for \(\cosh\): \[ \cosh(x)=\sum_{n=0}^\infty \dfrac{1}{(2n)!}x^{2n} \] is identical to that for \(\cos\): \[ \cos(x)=\sum_{n=0}^\infty \dfrac{(-1)^n}{(2n)!}x^{2n} \] except that there are no minuses. This is one of the reasons the name hyperbolic cosine includes the word cosine.
-
-
\(f(x)=x\cos(x^2)\)
Start with the series: \[ \cos x=\sum_{k=0}^\infty (-1)^k\dfrac{x^{2k}}{(2k)!} =1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\cdots \]
\(\displaystyle x\cos x^2=\sum_{k=0}^\infty (-1)^k\dfrac{x^{4k+1}}{(2k)!} =x-\dfrac{x^5}{2!}+\dfrac{x^9}{4!}-\cdots \)
We start with the series for cosine: \[ \cos x=\sum_{k=0}^\infty (-1)^k\dfrac{x^{2k}}{(2k)!} =1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\cdots \] We substitute \(x\to x^2\): \[ \cos x^2=\sum_{k=0}^\infty (-1)^k\dfrac{x^{4k}}{(2k)!} =1-\dfrac{x^4}{2!}+\dfrac{x^8}{4!}-\cdots \] Finally, we multiply by \(x\): \[ x\cos x^2=\sum_{k=0}^\infty (-1)^k\dfrac{x^{4k+1}}{(2k)!} =x-\dfrac{x^5}{2!}+\dfrac{x^9}{4!}-\cdots \]
-
\(f(x)=\cos^2(x)\)
Use \(\displaystyle \cos^2x=\dfrac{1+\cos2x}{2}\)
\(\displaystyle \cos^2x =\dfrac{1+\cos 2x}{2} =1+\sum_{n=1}^\infty (-1)^n\dfrac{2^{2n-1}x^{2n}}{(2n)!}\)
We use the identity \(\cos^2x=\dfrac{1+\cos 2x}{2}\). We start with the series for \(\cos x\): \[ \cos x=\sum_{n=0}^\infty (-1)^n\dfrac{x^{2n}}{(2n)!} =1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\cdots \] We substitute \(x\to 2x\): \[\begin{aligned} \cos 2x&=\sum_{n=0}^\infty (-1)^n\dfrac{(2x)^{2n}}{(2n)!} =1-\dfrac{(2x)^2}{2!}+\dfrac{(2x)^4}{4!}-\cdots \\ &=\sum_{n=0}^\infty (-1)^n\dfrac{2^{2n}x^{2n}}{(2n)!}= 1-2x^2+\dfrac{2}{3}x^4-\cdots \\ \end{aligned}\] We add \(1\) and divide by \(2\). First in expanded form: \[ \cos^2x=\dfrac{1+\cos 2x}{2} =1-x^2+\dfrac{1}{3}x^4-\cdots \] Now in summation form: (Notice how we separate the \(n=0\) term from the rest of the sum.) \[\begin{aligned} 1+\cos 2x &=2+\sum_{n=1}^\infty (-1)^n\dfrac{2^{2n}x^{2n}}{(2n)!} \\ \cos^2x =\dfrac{1+\cos 2x}{2} &=1+\sum_{n=1}^\infty (-1)^n\dfrac{2^{2n-1}x^{2n}}{(2n)!} \end{aligned}\]
-
\(f(x)=x^3e^{x^2}\)
\(\displaystyle x^3e^{x^2}=\sum_{n=0}^\infty\dfrac{x^{2n+3}}{n!} =x^3+x^5+\dfrac{x^7}{2}+\dfrac{x^9}{3!}+\cdots \)
We start with the series for \(e^x\): \[\begin{aligned} e^x &=\sum_{n=0}^\infty \dfrac{x^n}{n!} \\ &=1+x+\dfrac{x^2}{2}+\dfrac{x^3}{3!}+\cdots \end{aligned}\] To get \(e^{x^2}\) from \(e^x\), we substitute \(x^2\) for \(x\): \[\begin{aligned} e^{x^2}&=\sum_{n=0}^\infty\dfrac{x^{2n}}{n!} \\ &=1+x^2+\dfrac{x^4}{2}+\dfrac{x^6}{3!}+\cdots \end{aligned}\] Finally, we must multiply by \(x^3\), giving us \[\begin{aligned} x^3e^{x^2}&=\sum_{n=0}^\infty\dfrac{x^{2n+3}}{n!} \\ &=x^3+x^5+\dfrac{x^7}{2}+\dfrac{x^9}{3!}+\cdots \end{aligned}\]
-
\(f(x)= \begin{cases} \dfrac{1-\cos x}{x^2} \quad&\text{if}& x\neq 0 \\ \dfrac{1}{2}& \text{if}& x=0 \end{cases} \)
In the series for \(\cos x\) split off the constant term so you can combine it with the \(1\).
\(\begin{aligned}\displaystyle f(x)&= \begin{cases} \dfrac{1-\cos x}{x^2} \quad&\text{if}& x\neq 0 \\ \dfrac{1}{2}& \text{if}& x=0 \end{cases} \\ &=\sum_{n=1}^\infty (-1)^{n+1}\dfrac{x^{2n-2}}{(2n)!} \\ &=\dfrac{1}{2}-\dfrac{x^2}{4!}+\dfrac{x^4}{6!}-\cdots \end{aligned}\)
In the series for cosine we split off the constant term because we will need to subtract from \(1\): \[\begin{aligned} \cos x&=\sum_{n=0}^\infty (-1)^n\dfrac{x^{2n}}{(2n)!} =1+\sum_{n=1}^\infty (-1)^n\dfrac{x^{2n}}{(2n)!} \\ &=1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\dfrac{x^6}{6!}+\cdots \end{aligned}\] Then, we subtract from \(1\): \[\begin{aligned} 1-\cos x&=-\sum_{n=1}^\infty (-1)^n\dfrac{x^{2n}}{(2n)!} =\sum_{n=1}^\infty (-1)^{n+1}\dfrac{x^{2n}}{(2n)!} \\ &=\dfrac{x^2}{2!}-\dfrac{x^4}{4!}+\dfrac{x^6}{6!}-\cdots \end{aligned}\] Finally, we divide by \(x^2\): \[\begin{aligned} \dfrac{1-\cos x}{x^2} &=\sum_{n=1}^\infty (-1)^{n+1}\dfrac{x^{2n-2}}{(2n)!} \\ &=\dfrac{1}{2}-\dfrac{x^2}{4!}+\dfrac{x^4}{6!}-\cdots \end{aligned}\] When \(x=0\), the series becomes equal to \(\dfrac{1}{2}\), so this is the series for \(f(x)\).
-
\(f(x)= \begin{cases} \dfrac{1-e^{-x}}{x} \quad&\text{if}& x\neq 0 \\ 1& \text{if}& x=0 \end{cases} \)
\(\begin{aligned}\displaystyle \dfrac{1-e^{-x}}{x} &=\sum_{n=1}^\infty \dfrac{(-1)^{n-1} x^{n-1}}{n!} =\sum_{k=0}^\infty \dfrac{(-1)^k x^k}{(k+1)!} \\ &=1-\dfrac{x}{2}+\dfrac{x^2}{3!}+\cdots \end{aligned}\)
We start with the series for \(e^x\): \[\begin{aligned} e^x &=\sum_{n=0}^\infty \dfrac{x^n}{n!} \\ &=1+x+\dfrac{x^2}{2}+\dfrac{x^3}{3!}+\cdots \end{aligned}\] Next, we replace \(x\) by \(-x\) and then split off the constant term: \[\begin{aligned} e^{-x} &=\sum_{n=0}^\infty \dfrac{(-x)^n}{n!} =1+\sum_{n=1}^\infty \dfrac{(-1)^n x^n}{n!} \\ &=1-x+\dfrac{x^2}{2}-\dfrac{x^3}{3!}+\cdots \end{aligned}\] Then, we subtract it from \(1\): \[\begin{aligned} 1-e^{-x} &=-\sum_{n=1}^\infty \dfrac{(-1)^n x^n}{n!} =\sum_{n=1}^\infty \dfrac{(-1)^{n-1} x^n}{n!} \\ &=x-\dfrac{x^2}{2}+\dfrac{x^3}{3!}+\cdots \end{aligned}\] Finally, we divide it by \(x\), getting \[\begin{aligned} \dfrac{1-e^{-x}}{x} &=\sum_{n=1}^\infty \dfrac{(-1)^{n-1} x^{n-1}}{n!} \\ &=1-\dfrac{x}{2}+\dfrac{x^2}{3!}+\cdots \end{aligned}\] At \(x=0\), this series converges to \(1\), so this is also the series for \(f(x)\). Finally, in the summation form we can shift the index by setting \(k=n-1\). Then \[ \dfrac{1-e^{-x}}{x} =\sum_{k=0}^\infty \dfrac{(-1)^k x^k}{(k+1)!} \]
-
\(f(x)=\cos(\sqrt{x})\)
\(\displaystyle \cos \sqrt{x}=\sum_{k=0}^\infty (-1)^k\dfrac{x^{k}}{(2k)!} =1-\dfrac{x}{2!}+\dfrac{x^2}{4!}-\cdots\)
We start with the series for \(\cos x\): \[ \cos x=\sum_{k=0}^\infty (-1)^k\dfrac{x^{2k}}{(2k)!} =1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\cdots \] Then, we substitute \(x\to \sqrt{x}\): \[ \cos \sqrt{x}=\sum_{k=0}^\infty (-1)^k\dfrac{x^{k}}{(2k)!} =1-\dfrac{x}{2!}+\dfrac{x^2}{4!}-\cdots \]
-
Consider the function \(\tan x\).
-
Find the \(5^\text{th}\) degree Maclaurin polynomial for \(\tan x\).
Find the terms of the series from the definition.
\(\displaystyle T_5\tan(x)=x+\dfrac{1}{3}x^3+\dfrac{2}{15}x^5\)
The function and \(5\) derivatives and their values at \(x=0\) are: \[\begin{aligned} f(x)&=\tan x &f(0)&=0 \\[2pt] f'(x)&=\sec^{2} x &f'(0)&=1 \\[2pt] f''(x)&=2\tan x\sec^{2} x &f''(0)&=0 \\[2pt] f'''(x)&=2\sec^{2} x(2\tan^{2} x+\sec^{2} x) &f'''(0)&=2\\[2pt] f^{(4)}(x)&=8\tan x\sec^{2} x(\tan^{2} x+2\sec^{2} x) &f^{(4)}(0)&=0 \\[2pt] f^{(5)}(x)&=8\sec^{2} x(2\sec^{4} x+11\sec^{2} x\tan^{2} x+2\tan^{4} x) &f^{(5)}(0)&=16 \end{aligned}\] Notice that the even derivatives are all \(0\). Thus, the \(5^\text{th}\) degree Maclaurin polynomial for \(\tan x\) is: \[\begin{aligned} T_5f(x)&=f(0)+f'(0)x+\dfrac{f''(0)}{2}x^2 \\ &\quad+\dfrac{f'''(0)}{3!}x^3+\dfrac{f^{(4)}}{4!}x^4+\dfrac{f^{(5)}}{5!}x^5 \\ T_5\tan(x)&=x+\dfrac{1}{3}x^3+\dfrac{2}{15}x^5 \end{aligned}\]
jp
-
Use the \(5^\text{th}\) degree Maclaurin polynomial for \(\tan x\) to approximate \(\tan(0.1)\).
\(\displaystyle \tan(0.1)\approx T_5\tan(0.1)=0.10033467\)
We found: \[ T_5\tan(x)=x+\dfrac{1}{3}x^3+\dfrac{2}{15}x^5 \] We plug in \(x=.1\): \[ \tan(0.1)\approx T_5\tan(0.1)=0.1+\dfrac{1}{3}0.1^3+\dfrac{2}{15}0.1^5 =0.10033467 \]
A calculator says \(\tan(0.1)=0.1003346721\). So \(T_5\tan(0.1)=0.10033467\) is an excellent approximation. The plot shows \(\tan(x)\) in blue and \(T_5\tan(x)\) in red. The values at \(x=.1\) are indistinguishable.
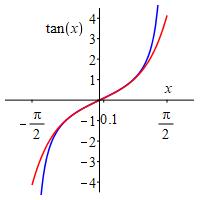
-
-
Use the \(7^\text{th}\) degree Maclaurin polynomial for \(\ln(1+x)\) to approximate \(\ln(1.1)\).
\(\displaystyle \ln(1.1)\approx T_7\ln(1+.1) =0.09531018095\)
In a previous problem, we found the Maclaurin series for \(\ln(1+x)\): \[\begin{aligned} \ln(1+x) &=\sum_{n=1}^\infty \dfrac{(-1)^{n+1}}{n}x^n \\ &=x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\dfrac{x^4}{4}+\dfrac{x^5}{5}-\dfrac{x^6}{6}+\dfrac{x^7}{7}+\cdots \end{aligned}\] So the \(7^\text{th}\) degree Maclaurin polynomial is: \[ T_7\ln(1+x) =x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\dfrac{x^4}{4}+\dfrac{x^5}{5}-\dfrac{x^6}{6}+\dfrac{x^7}{7} \] We plug in \(x=.1\): \[\begin{aligned} \ln(1.1)&\approx \left.T_7\ln(1+x)\right|_{x=.1} \\ &=.1-\dfrac{.1^2}{2}+\dfrac{.1^3}{3}-\dfrac{.1^4}{4}+\dfrac{.1^5}{5}-\dfrac{.1^6}{6}+\dfrac{.1^7}{7} \\ &=0.0953101809 \end{aligned}\]
A calculator says \(\ln(1.1)=0.09531017980\). So \(\left.T_7\ln(1+x)\right|_{x=.1}=0.09531018095\) is an excellent approximation. The plot shows \(\ln(1+x)\) in blue and \(T_7\ln(1+x)\) in red. The values at \(x=.1\) are indistinguishable.
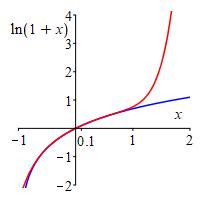
-
The Maclaurin series for \(f(x)=\cosh x=\dfrac{e^x+e^{-x}}{2}\) is \[ Tf(x)=\sum_{n=0}^{\infty} \dfrac{1}{(2n)!}x^{2n} =1+\dfrac{1}{2!}x^2+\dfrac{1}{4!}x^4+O(x^6) \] If the \(2^\text{nd}\) degree Taylor polynomial, \(T_2f(x)=1+\dfrac{1}{2!}x^2\), is used to approximate \(\cosh(2)\), use the Taylor Remainder Theorem to find a bound on the absolute value of the Taylor remainder, \(|R_2f(2)|\). Here are two plots which may be useful:
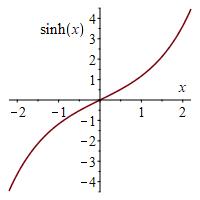
\(\displaystyle |R_{2}f(2)| \le \dfrac{\sinh2}{3!}2^3\approx4.84 \)
The Remainder is: \[ R_{2}f(x) =\dfrac{f'''(c)}{3!}(x-a)^3 \] for some \(c\) between \(a\) and \(x\). Here \(a=0\) and \(x=2\). So: \[ R_{2}f(2)=\dfrac{f'''(c)}{3!}2^3 \] for some \(c\in[0,2]\). We compute the derivatives of \(f(x)=\cosh x\): \[ f'(x)=\sinh x \qquad f''(x)=\cosh x \qquad f'''(x)=\sinh x \] Since \(\sinh x\) is increasing (See the plot.) and \(c\in[0,2]\), the maximum of \(f'''(c)=\sinh c\) is \(\sinh2\). So: \[ |R_{2}f(2)| \le \dfrac{\max|f'''(c)|}{3!}2^3=\dfrac{\sinh2}{3!}2^3 \approx4.84 \]
-
Find the Taylor series for \(f(x)=\cos(x)\) centered at \(x=\dfrac{\pi}{4}\) and its radius of convergence.
The Taylor series is \[ T\cos(x) =\sum_{k=0}^\infty \dfrac{(-1)^k\sqrt{2}}{(2k)!\cdot 2}\left(x-\dfrac{\pi}{4}\right)^{2k} +\sum_{k=0}^\infty \dfrac{(-1)^{k+1}\sqrt{2}}{(2k+1)!\cdot 2}\left(x-\dfrac{\pi}{4}\right)^{2k+1} \] and the radius of convergence is \(R=\infty\).
The function, its derivatives and their values at \(x=\dfrac{\pi}{4}\) are: \[\begin{aligned} f(x)&=\cos(x) &f\left(\dfrac{\pi}{4}\right)&=\dfrac{\sqrt{2}}{2} \\[2pt] f'(x)&=-\sin(x) &f'\left(\dfrac{\pi}{4}\right)&=-\dfrac{\sqrt{2}}{2} \\[2pt] f''(x)&=-\cos(x)\qquad &f''\left(\dfrac{\pi}{4}\right))&=-\dfrac{\sqrt{2}}{2} \\[2pt] f'''(x)&=\sin(x) &f'''\left(\dfrac{\pi}{4}\right)&=\dfrac{\sqrt{2}}{2}\\[2pt] f^{(4)}(x)&=\cos(x) &f^{(4)}\left(\dfrac{\pi}{4}\right)&=\dfrac{\sqrt{2}}{2} \end{aligned}\] Note that the pattern is positive, negative, negative, positive, positive, negative, negative, positive, positive... We plug these into the Taylor polynomial centered at \(x=\dfrac{\pi}{4}\): (Don't forget the factorials.) \[\begin{aligned} f(x) &=f\left(\dfrac{\pi}{4}\right)+f'\left(\dfrac{\pi}{4}\right)\left(x-\dfrac{\pi}{4}\right) +\dfrac{f''\left(\dfrac{\pi}{4}\right)}{2}\left(x-\dfrac{\pi}{4}\right)^2 \\ &\quad+\dfrac{f'''\left(\dfrac{\pi}{4}\right)}{3!}\left(x-\dfrac{\pi}{4}\right)^3 +\dfrac{f^{(4)}\left(\dfrac{\pi}{4}\right)}{4!}\left(x-\dfrac{\pi}{4}\right)^4+\cdots \\ \cos(x)&=\dfrac{\sqrt{2}}{0!\cdot 2} -\dfrac{\sqrt{2}}{1!\cdot 2}\left(x-\dfrac{\pi}{4}\right) -\dfrac{\sqrt{2}}{2!\cdot 2}\left(x-\dfrac{\pi}{4}\right)^2 \\ &\quad+\dfrac{\sqrt{2}}{3!\cdot 2}\left(x-\dfrac{\pi}{4}\right)^3 +\dfrac{\sqrt{2}}{4!\cdot 2}\left(x-\dfrac{\pi}{4}\right)^4+\cdots \end{aligned}\] To generalize the sequence, we need to look separately at the odd and even terms. For the even terms, \(n=2k\), the \(n^\text{th}\) derivative is \[\begin{aligned} f^{(n)}(x)&=f^{(2k)}(x)=(-1)^k\cos(x) \\ f^{(n)}\left(\dfrac{\pi}{4}\right) &=f^{(2k)}\left(\dfrac{\pi}{4}\right)=(-1)^k\dfrac{\sqrt{2}}{2} \end{aligned}\] and the \(n^\text{th}\) term in the Taylor series is \[\begin{aligned} \dfrac{f^{(n)}\left(\dfrac{\pi}{4}\right)}{n!}\left(x-\dfrac{\pi}{4}\right)^n =\dfrac{(-1)^k\sqrt{2}}{(2k)!\cdot 2}\left(x-\dfrac{\pi}{4}\right)^{2k} \end{aligned}\] Similarly, for the odd terms, \(n=2k+1\), the \(n^\text{th}\) derivative is \[\begin{aligned} f^{(n)}(x)&=f^{(2k+1)}(x)=(-1)^{k+1}\sin(x) \\ f^{(n)}\left(\dfrac{\pi}{4}\right) &=f^{(2k+1)}\left(\dfrac{\pi}{4}\right)=(-1)^{k+1}\dfrac{\sqrt{2}}{2} \end{aligned}\] and the \(n^\text{th}\) term in the Taylor series is \[\begin{aligned} \dfrac{f^{(n)}\left(\dfrac{\pi}{4}\right)}{n!}\left(x-\dfrac{\pi}{4}\right)^n =\dfrac{(-1)^{k+1}\sqrt{2}}{(2k+1)!\cdot 2}\left(x-\dfrac{\pi}{4}\right)^{2k+1} \end{aligned}\] Putting these together, the Taylor series is \[\begin{aligned} T&\cos(x) =\sum_{n=0}^\infty \dfrac{f^{(n)}\left(\dfrac{\pi}{4}\right)}{n!}\left(x-\dfrac{\pi}{4}\right)^n \\ &=\sum_{k=0}^\infty \dfrac{f^{(2k)}\left(\dfrac{\pi}{4}\right)}{(2k)!}\left(x-\dfrac{\pi}{4}\right)^{2k} +\sum_{k=0}^\infty \dfrac{f^{(2k+1)}\left(\dfrac{\pi}{4}\right)}{(2k+1)!}\left(x-\dfrac{\pi}{4}\right)^{2k+1} \\ &=\sum_{k=0}^\infty \dfrac{(-1)^k\sqrt{2}}{(2k)!\cdot 2}\left(x-\dfrac{\pi}{4}\right)^{2k} +\sum_{k=0}^\infty \dfrac{(-1)^{k+1}\sqrt{2}}{(2k+1)!\cdot 2}\left(x-\dfrac{\pi}{4}\right)^{2k+1} \end{aligned}\] To find the radius of convergence, we use the ratio test, but apply it separately to the even and odd terms. For the even terms: \[\begin{aligned} \rho&=\lim_{k\to\infty}\dfrac{|a_{k+1}|}{|a_k|} =\lim_{k\to\infty} \dfrac{\left|x-\dfrac{\pi}{4}\right|^{2k+2}\sqrt{2}}{(2k+2)!\cdot 2} \dfrac{(2k)!\cdot 2}{\left|x-\dfrac{\pi}{4}\right|^{2k}\sqrt{2}} \\ &=\left|x-\dfrac{\pi}{4}\right|^2\lim_{k\to\infty} \dfrac{1}{(2k+2)(2k+1)}=0 \end{aligned}\] For the odd terms: \[\begin{aligned} \rho&=\lim_{k\to\infty}\dfrac{|a_{k+1}|}{|a_k|} =\lim_{k\to\infty} \dfrac{\left|x-\dfrac{\pi}{4}\right|^{2k+3}\sqrt{2}}{(2k+3)!\cdot 2} \dfrac{(2k+1)!\cdot 2}{\left|x-\dfrac{\pi}{4}\right|^{2k+1}\sqrt{2}} \\ &=\left|x-\dfrac{\pi}{4}\right|^2\lim_{k\to\infty} \dfrac{1}{(2k+3)(2k+2)}=0 \end{aligned}\] Since \(\rho=0 \lt 1\) for all \(x\), the series converges for all \(x\) and the radius of convergence is \(R=\infty\).
dd/jp
In these exercises, write out the terms of the Taylor series for \(f(x)\) centered at \(x=2\) up to and including the \(4^\text{th}\) degree term.
In the next exercises, find the Taylor series for \(f(x)\) and find its radius of convergence. (Write out the series up to the \(4^\text{th}\) or \(5^\text{th}\) degree; then find the summation form with the general term and use that to find the radius of convergence.)
In the following exercises, verify the that the special Maclaurin series (Taylor series centered at \(x=0\)) given in the chapter are correct. Then find its radius of convergence. (Write out the series up to \(4^\text{th}\) or \(5^\text{th}\) degree and then find the summation form with the general term.)
In these exercises, use the standard Maclaurin series to construct the Maclaurin series of the given function.
If a function \(f(x)\) is approximated by its \(k^\text{th}\) degree Taylor polynomial: \[ T_{k}f(x)=\sum_{n=0}^{k}\dfrac{f^{(n)}(a)}{n!}(x-a)^n \] then the Taylor remainder \(R_{k}f(x)=f(x)-T_{k}f(x)\) is: \[ R_{k}f(x)=\dfrac{f^{(k+1)}(c)}{(k+1)!}(x-a)^{k+1} \] for some \(c\) between \(a\) and \(x\).
Challenge Exercise
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum